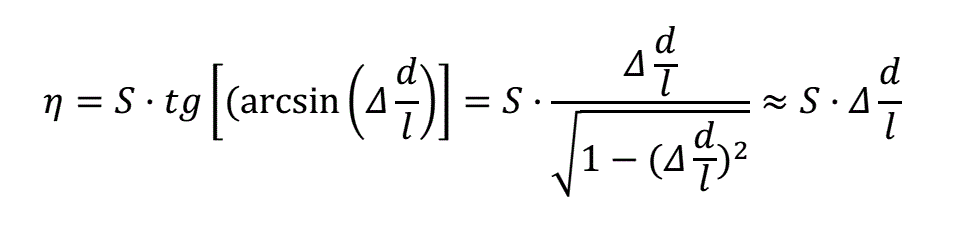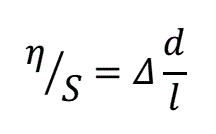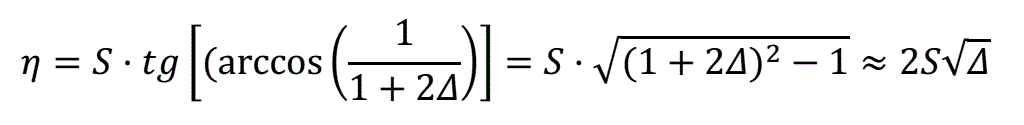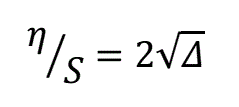| Home » Articles » Theoretical papers » Coilgun calculations |
As gauss-building comes forward, new and new models appear with relatively high initial velocities, I think it’s time to rise the question about accuracy of coilguns. To answer this question one should at first mention the important fact: in contrast to pneumatic and firearms, the projectile in coilguns is moving inside barrel with some gap (i.e. the diameter of the projectile is a bit smaller than one of the barrel). The reason is simple – it is just a way to reduce friction which degrades efficiency of acceleration (not so large itself). Let us consider the gap as δ, and its relation to the diameter of projectile d as ∆, and look how these values influence the accuracy of shooting. At first let’s analyze a cylindrical projectile with length of l:
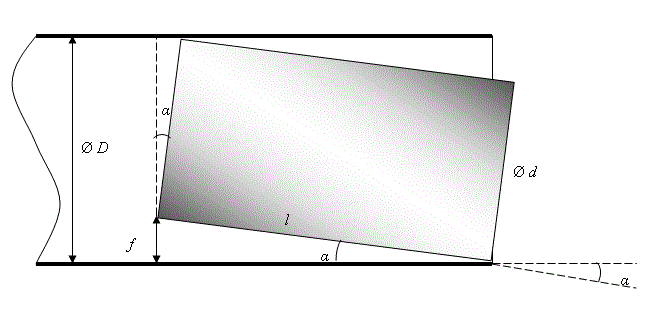
Fig. 1. The picture shows that the projectile leaving the barrel with deviation angle α has a gap between his rear end and the barrel, which is calculated as: f = l ·sin α = D - d ·cos α (1)
Then, considering small α (i.е. cos α ≈1), we easily get
α = arcsin (δ/l)= arcsin {∆(d/l)} (2)
The same situation for spherical projectile (fig .2):
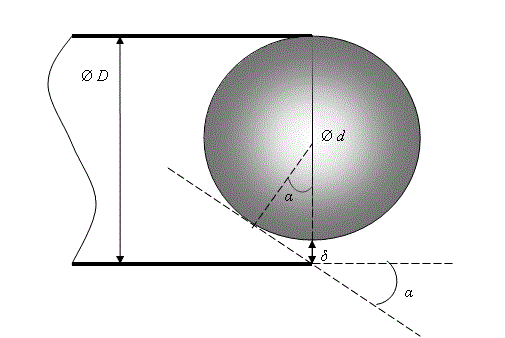
Fig. 2. Now the trajectory of maximal deviation will be the tangent to the sphere crossing the end of barrel, and deflection angle is:
α = arccos {d/(d+2δ)}= arccos {1/(1+2∆)} (3)
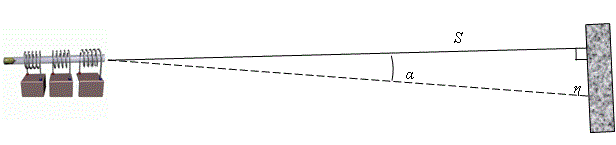
Let’s find out how the deviation η on distance S is related to α (fig. 3):
Fig. 3. It is seen that
η = S∙tg(α) (4)
Inserting equations (1) and (2) for α to (3), one will get according to known trigonometric formulae and assuming ∆<<1: - for cylindrical projectile:
(5)
or
(5a) - for spherical projectile:
(6)
(6a)
As we can see, deviation is proportional to ∆ in first case , and to square root of ∆ in latter one. As ∆<<1, it is already clear that deviation for the spherical projectile is much larger. Now let’s do some quantitative estimations: Suggest, we have 8 mm caliber projectile and gap of 50 microns ( in real amateur coilguns the gap makes 100 microns and more because of many reasons, the main of them - low rigidity and roughness of thin-wall tubes which the barrels are made of). Then ∆ = 0,00625 and shooting at 10 m we shall have maximum scattering of 1,58 m for spherical projectile! The cylindrical one with diameter-to-length ratio of 1/3 in the same conditions will give only 2,1 cm deviation. Of course, these values are only qualitive, as the projectiles must not always fly along the trajectories of maximum deviation depicted earlier, but the tendency is clear - the deviation for cylinder is much smaller than for ball. It is intuitively obvious because elongated cylindrical body plays a role of "stabilizer" preventing projectile from large deviation while leaving a barrel. It is interesting to compare these speculative assessments to real experiments dedicated to investigations of accuracy of EM-3 coilgun which are situated here. It this case we have cylindrical projectile of 5.5 mm caliber and d/l ratio of about 0.035, moving inside barrel of 5.9 mm inside diameter. According to (5), we get 2.56 cm deviation on 10 m distance, which perfectly coincides to the experimental results (2.5 cm scattering in single-arrow shooting). Such a precise agreement is of course accidental because we didn't account for many factors (for example flexibility of arrow in this specific case), but it illustrates correctness of the suggested method.
| |
| Views: 718 | |
| Total comments: 0 | |