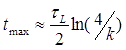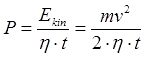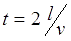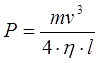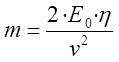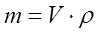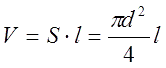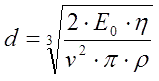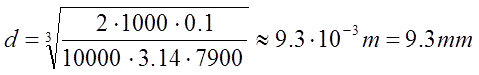| Home » Articles » Theoretical papers » Coilgun calculations |
1. Assessment of current. We often need to suggest a value of current in a coil of gauss-gun i, given deposited energy is E. This can be performed by following simple equation. Other parameters are coil length l, projectile velocity v and capacitor voltage U. Then: i ≈ (E·v)/(U·l) The formula is precise when its components are constant. Thus, it works best for middle and last coils of multistage accelerator fed by common capacitor, where velocity and voltage change negligbly.
2. Point of maximum current. It is sometimes necessary to determine a moment of time when curent in a coil achieves its maximal value. This moment is described by the next complicated equation (as it is shown here):
where
R, C, L - resistance, capacitance and inductance, respectively, arth - hyperbolic arctangent ( arth (x) = ½ln {(1+x)/(1-x)} ). Fortunately, this formula can be substantially simplified for strongly overdamped systems, where k<<1. This case realizes in high-capacity circuits (e.g. multistage coilguns driven by common capacitor) or in single stage gauss guns with thin coils (i.e. large length-to-diameter and length-to-thickness ratio). Alas, decomposing the equation above to Taylor series and neglecting the second-order terms, we have just:
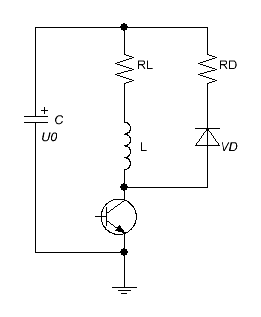
3. Assessment of damping resistor. If a closeable switch circuit is utilized, it is necessary to properly choose a value of damping resistor in R-D-chian which limits the inductive voltage spike.
It can be made as following. Maximum current obtained in RLC-circuit is no more than imax=U0/RL (where U0 is initial cap voltage, RL - active resistance of the chain including wire, switch resistance, parasitic elements etc). Then the voltage spike on the switch makes no more than Uk =U0+imaxRD=U0+U0·RD/RL. Thus, the damping resistance is RD = (Uk - U0)·RL/U0. Uk here is maximum voltage rating for the switch according to its datasheet.
4. Power (current) dependence on output velocity of a projectile. Suggest we have a linear accelerator of lenth l, giving speed v to a projectile of mass m (i.e. kinetic energy Ekin = mv2/2). Then the electric power spent during accelerarion is
where η is acceleration efficiency (considered a constant which is close to true for gauss guns with fixed dimensions), t is duration of acceleration process. Considering a uniform accelerated movement, we can write
So the equation for power becomes
Thus, the electric power consumed in a coilgun with fixed acceleration path is proportional to a cube of the output velocity. The same is true for current consumption supplied the voltage is nearly constant during the acceleration.
5. Assessment of a caliber of an electromagnetic accelerator. Consider we begin constructing a new coilgun. Basing on its mass and size, we can suggest energy capacity E0 and approximate efficiency η. Having planned to get an output velocity of v, what should be the caliber d? This question can be answered as follows. A mass of the projectile may calculated as
From another side, it is proportional to a volume and density p of the bullet's material:
It is simple to find the volume of a cylindrical body by its area and length:
At last, the length must be limited by fourfold diameter (otherwise the efficiency of acceleration degrades seriously): l ≈ 4 d. Combining the equations above, we can finally get the following assesment for the diameter of the projectile:
Taking a shorter bullet, we may obtain some higher caliber, but not much more (in 21/3 times). For instance, l ≈ 2 d gives only 26 % rise to the diameter.
Example: we want to obtain 100 m/s from 1000 J capacitor bank with approx. 10 % efficiency and iron (p = 7900 kg/m3). Then
| |||
| Views: 1210 | | |||
| Total comments: 0 | |
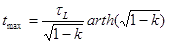
 is capacitive constant of the circiut,
is capacitive constant of the circiut,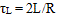 inductive constant,
inductive constant, damping factor,
damping factor,