This calculation is dedicated to the major question - what can be efficiency of a gauss gun?
It is a kind of "holy Grail" of gauss-building - each constructor wants to know if the parameters of his coilgun are close to optimal ones and what should he do to increase efficiency. There are two ways to solve this problem - practical and theoretical. From a practical point of view, FEMM modelling can be pricelessly helpful. A lot of scripts have been made for simulation of various coilgun configurations (including varying parameters), some of them are listed in Petrovich's page. But that is the problem that one needs to sweep all the parameters to be sure that the main, not local, maximum is caught. For example, having found an optimal initial position of a projectile and corresponding peak efficiency, we should vary the other conditions (wire gauge etc) to make sure that the answer would not change.
As a result, the solution is quite laborious and I don't know any such a full calculation yet.
The theoretical approach can be as follows. We know that the accelerating force is proportional to the inductance gradient:
F ~ ½ i 2 dL/dx (1)
The gradient grows when magnetic permeability of material of the projectile increases. The latter drops with magnetic field H increase, so the efficiency of the system must decrease with H (i.e. coil current or energy deposition during a shot).
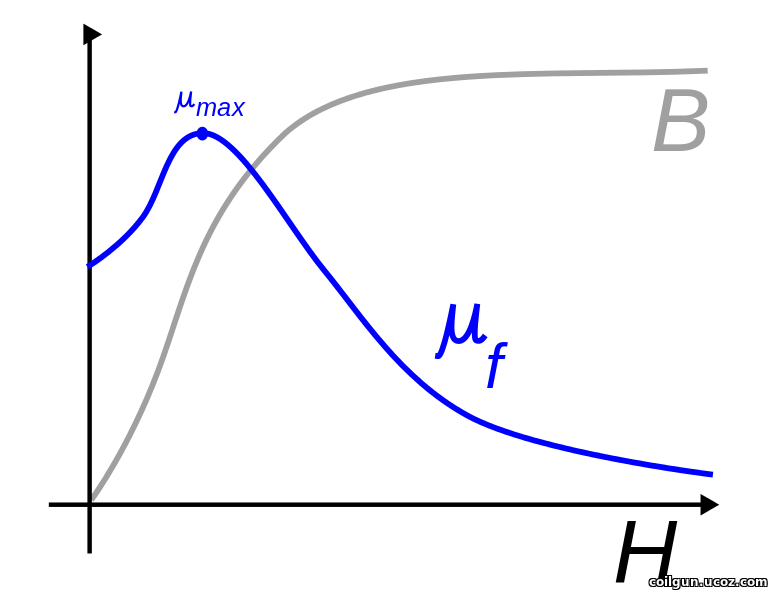 |
Fig. 1. Magnetic permeability of ferromagnetics (https://en.wikipedia.org/wiki/Permeability_(electromagnetism) )
|
Such dependence indeed occurs in most cases, so decreasing energy is considered to be "panacea" to obtain high efficiency. Two difficulties are here. First, decreasing energy is equivalent to degrading velocity, i.e. the projectile is accelerated more efficiently but slower, so we must build up additional stages to hold constant muzzle velocity. This process cannot be infinite and sooner or later we would face the limitations inherent to portative systems (I write more about this situation here). Second, the previous picture shows a peak in permeability in low fields, so the efficiency vs energy dependence must have a maximum, too (although this should be clear in very low energy systems only).
Another approach is like this. It is known (see here and here) that acceleration efficiency depends on electromotive force induced in a coil by moving projectile ("inductive voltage"). This voltage is proportional to magnetic flux rate i.e.to projectile velocity:
eind ~ dx/dt (2)
That's why multistage coilguns are generally much more efficient than the single-coil ones.
But considering a first stage (with zero initial velocity), a paradox arises: from one side, we should decrease energy to hold high efficiency, form another side, following (2), we should try to accelerate a projectile as fast as it is possible, which is equivalent to higher energy consumption. So it must be concluded that the efficiency vs energy curve cannot be monotonic.
I conducted a vast volume of FEMM simulations to determine an influence of eneggy on ecoilgun efficiency. The object was simple transistor-driven coil, modelled by specially desiged script coilgun_107_trans_ind.lua. Its feature is variation of inductive voltage spike at the transistor when it is closed. This parameter impacts the efficiency considerably, because the highe the spike can be - the closer the projectile may be situated to the zero-force point (a middle of coil) which is close to maximum force point.
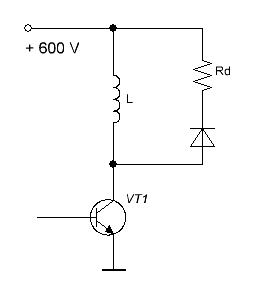 |
Fig. 2. One-stage schematic used for simulation. |
As the spike is determined by damping resistor Rd, this parameter is called "damper" further. Two values of damper were chosen: 1200 V (i.e. votlage at closing is twice the initial one), and 2400 V.
Other parameters varied were: wire gauge, outer coil diameter, moment of deactivation of the switch and initial position of the projectile. Their combination defined the energy consumption from the capacitor, which were set to some fixed points - 1 J, 3 J, 10 J, 30 J,100 J and 300 J. Such values let a graph to sweep over all the range by logarithmic scale.
The rest of initail conditions were:
- initial cap voltage - 600 V;
- capacitance - 800 mkF;
- parasitic resistance of the system - 50 mOhms;
- coil length - 50 mm;
- inside coil diameter - 20 mm;
- cylinrical projectile of 18 mm diameter.
So, it is rather high-bore system which is explained by my ineterst to such coilguns on that time. The second iteration was conducted for twice smaller 10 mm system to see how the result would change.
The conclusive graph after Excel processing is below.
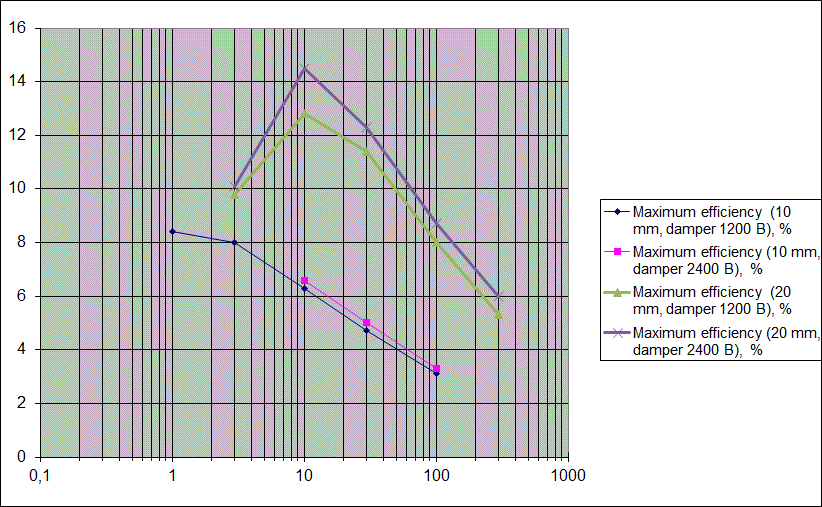
There is the evident peak in efficiency (in about 10 J for 20 mm system).
Other important results are as follows:
1) The peak is situated near 1 J for 10 mm (which is more realistic for practically built coilguns). The maximum efficiencies themselves are about 13 % for 20 mm and some hogher than 8 % for 10 mm systems, i.e. peak efficiences are not proportional to the caliber (they rgow slower).
2) Damper has little impact on efficiency. It is a substantial result as it allows to limit the nominal voltage of a switch (which is critical for total cost of the system).
3) The efficiency vs energy dependence is clearly logarithmic after the peak (i.e. the efficiency decreases inversely proportional to the logarithm of energy).
Sincerely yours, Eugen