| Home » Articles » Experiments » Other |
The other day I received a package from AliExpress, in which the previously ordered components for my new Gaussian were waiting for me - a battery, a memory for it and as many as 50 pieces of brand-new JCCON electrolytic capacitors with a nominal capacity of 220 UF and a voltage of 450V (in the photo they are in a bag). Taking advantage of this abundance of samples, I decided to measure the parameters of capacitors, not only capacitance, but also such values as equivalent series resistance (ESR) and mass. Of course, I did not master all 50 products, but 10 pieces were enough for normal statistics. Below are the results and what follows is discussed.
Measurements of electrical parameters were made using an APPA 703 type RLC meter - I described it in more detail in this article. A convenient thing. The mass was measured on an electronic scale with an accuracy of 0.1 g (see Fig. 2).
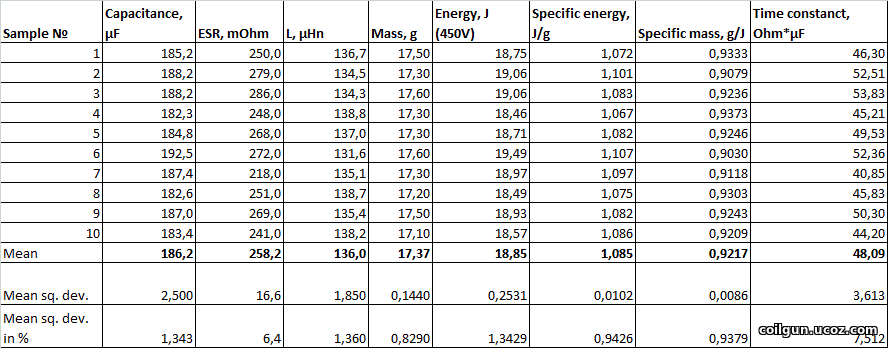
To begin with, I will give a general table with the results. In the last four columns, the outcomes of processing the received information are given - the accumulated energy of each capacitor at rated voltage, specific energy (per unit mass), specific mass (per unit energy - this is simply the inverse of the previous value), and the discharge time constant equal to the product of ESR and capacitance (this parameter illustrates the maximum achievable discharge rate of the capacitance at shot). In addition, the average values of the sample parameters and their spread were estimated (both in absolute value and as a percentage of the average, see the bottom 3 rows of the table). After the measurements, another experiment was conducted on the effect of holding the capacitors at rated voltage for 5..10 minutes. As it turned out, this had practically no effect on the parameter values, so these results are not displayed in the table. Fig. 3. The results.
What attracts attention? Firstly, all capacitances are noticeably lower than the nominal ones (on average, by 15%). This fits into the norms for electrolytic capacitors (usually - 20% of the nominal value is acceptable), but it certainly doesn't look very healthy for a batch of brand-new products... Secondly, the ESR turned out to be quite large - an average of 258 mOhm, which in combination with the measured capacitance gives an average value of the time constant of 48.1 ohms * UF. This is almost two and a half times more than the value that I give in this article based on measurements (almost 20 years ago) of several other lines of capacitors. Thirdly, the mass of the capacitors corresponds to their compactness and is surprisingly small, and accordingly, the specific energy capacity is quite large - more than 1 J/g. Thus, it can be concluded that the JCCON electrolytes purchased by me are rather not "low ESR", as it is written on them, but "low mass" or "high energy capacity"... It is interesting now to see how this will affect the parameters of the electromagnetic accelerator being developed. To do this, we will use the previously performed calculations regarding the limitations associated with the maximum mass of a portable capacitor bank, as well as the influence of ESR on the maximum achievable projectile velocity in a gaussgun with thyristor switching (this is exactly the model I'm going to do). It is quite simple with the mass - its value in the mentioned article was taken 3 g per 1 J of stored energy, and in the measured batch it turned out to be about 0.92 g. Therefore, in the same mass of the battery (its limit value was taken by me at the level of 6 kg), the accumulated energy will be more than 3 times higher. Because of this, it turns out that the limits associated with this factor disappear for all the considered cases of calibers and lengthes of accelerating coils (i.e., the blue coloring for the table in Fig. 3 is removed). In the case of ESR, the "forbidden zone" associated with the limitation of the projectile speed due to the internal resistance of the capacitors, on the contrary, will expand, because the ESR turned out to be larger than previously calculated, and this expansion turns out to be the most significant for small-caliber projectiles. The final view for the mentioned table is shown in Fig. 4. Let me remind you that the cells of the tables show the maximum velocity of the projectile (in m/s) achievable for a given caliber (d), outer diameter (D) and length (l) of the coil based on considerations of the shape of the current pulse in the coil and its twofold (first - acceleration, then, from a certain moment - braking) effects on the projectile.
As you can see, as a result of the adjustments made, larger calibers came out on top in terms of achievable speed, and first of all - 8 mm. In principle, this corresponds to the existing practice of Gauss-building, in which the most impressive results are achieved precisely for this (average) range of calibers. On the other hand, it would probably be premature to draw such global conclusions based on the analysis of a single line of capacitors, so on occasion I will try to expand the range of analyzed products and, accordingly, supplement this publication with fresh data.
Best regards, Yours Eugen
| ||||||||||||||||
| Views: 259 | | | ||||||||||||||||
| Total comments: 0 | |