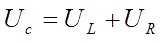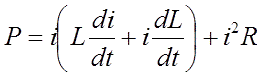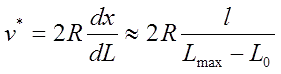| Home » Articles » Theoretical papers » Coilgun calculations |
Recently I found an interesting publication [1] inter alia describing an alrorithm of determination of so called "characteristic speed". This speed corresponds to velocity of the projectile when the efficiency of the accelerator increases to 50 % and more. Besides, the authors refer to earlier paper of the soviet scientists [2]. Their argumentation is briefly following: Kirchhoff's law for coilgun circuit is
where UC is stored capacitor voltage, UL and UR - inductive and resistive voltage drops, respectively. Multiplying both parts to current i and decomposing all the terms, the equation for power is derived:
Suggesting a multistage system with aprroximately constant current, we should write di/dt ≈ 0. Besides, let's remind an equation for mechanical power:
where v is velocity of the projectile, dL/dx - inductance gradient. It is clear that increasing the speed enlarges the power being absorbed by the projectile. Combining the equations above, we can get an expression for the speed when the ohmic dissipative power equals to kinetic power:
Here, the inductance change is expressed via the difference between its maximal value Lmax (with the projectile inside the coil) and minimal one L0 (without the projectile). l is length of the coil. v* in the previous equation is the "characteristic speed" (CS) itself. When the projectile moves faster than CS, it consumes more power than it is dissipated in wires. Obviously, if the accelerator is intended to have a substantially high efficiency, it must provide velocity v > v* along most of its length. The evaluations of CS for various types of electromagnetic accelerators can be found in literature, but I didn't discover it for reluctance accelerator. So, suggesting my own experience in gaussgun-building, I became interested in assessment of v* for the really constructed and well-calculated models. That's what I got:
It is clear from the table that we should have velocities of hundreds meters per second to obtain high-efficient coilguns. None of the enthusiast-built models have such parameters for today. However, there is no limitations to do that, and the only challenge is to assemble long enough accelerator equipped with a sufficient power source.
Note: the values in the table above are taken for coils in middle parts of the coilguns (4th coil for EM-3 and the coil with initial velocity of 30 m/s for EM-4). Inductances are calculated as one with projectile fully in the coil (Lmax) and one without the projectile (L0). All calculations are executed in FEMM.
Literature:
| |||||||||||||||||||
| Views: 908 | Comments: 3 | | |||||||||||||||||||
| Total comments: 3 | |
|
| |