| Home » Articles » Theoretical papers » Coilgun calculations |
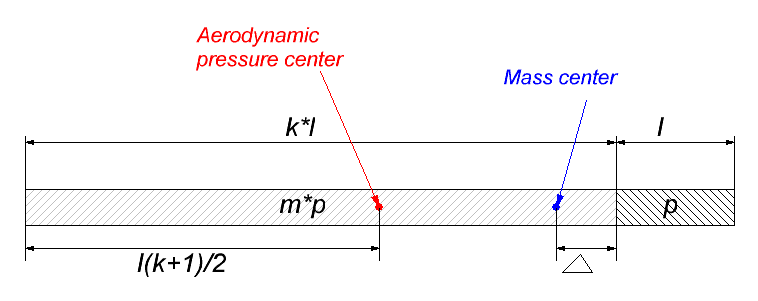
The aim of the investigation was to establish relations between length of head and tail of an unfinned arrow (for a crossbow or electromagnetic accelerator), and density of their materials. Lets look at this problem in more details. As it is known (for example, see here ) an arrow is aerodynamically stabilized when optimal positions of the mass center (MC) and aerodynamic force center (AFC) are achieved. Namely, the distance from nose to AFC must be at least twice the distance from nose to MC. Hereinafter we will consider an arrow with constant diameter along its length – this is the only type of arrow which can be used in coilguns (although crossbow bolts often have the tails which thicken to ends). In such situation MC is situated exactly in the middle of arrow. Suggesting the length of head to be l and the length of tail - k·l (i.e. the tail is k times longer than the head), and distance from MC to rear end of the head to be ∆, we will get following equation: l(1+k)>4(l+∆) (1) This is illustrated on picture below (hereinafter the tail and the head are simple cylinders). Besides, linear densities of materials of the head and tail are depicted as ρ and m·ρ, respectively.
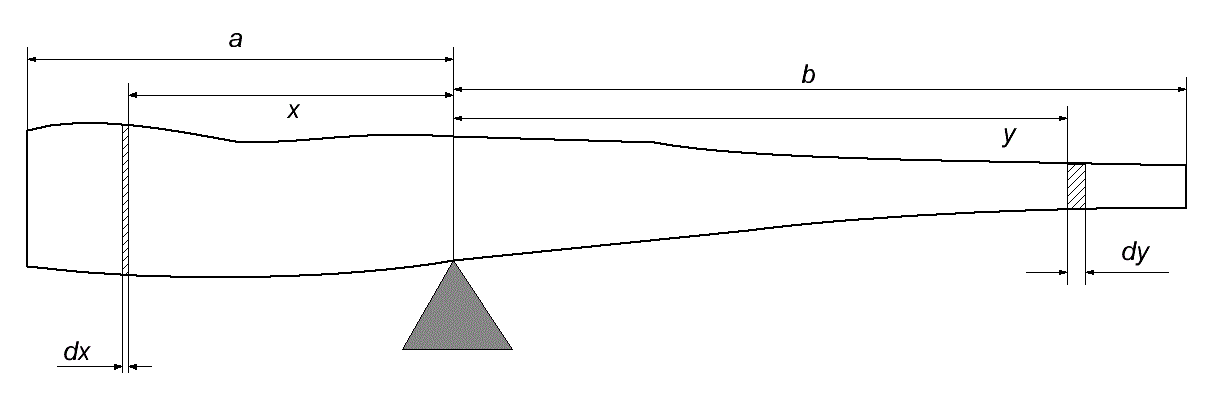
Fig. 1. Conditions of aerodynamic stabilization of an arrow. To go further we must understand how to determine exact position of MC. Let us imagine some prolonged body, balancing on a point pivot (fig. 2). Variation of linear density of the body is here achieved by variation of its diameter (not its material), but it doesn’t change the concept.
Fig. 2. Balancing of a body with varying linear density. Remember the school physics: the pivot will be in MC, if the summary force momentum from the body is zero. Mathematically it is written as:
Considering our mixed-materials case, this equation will be:
When MC is inside the head (i.e. ∆ < 0), some modifications take place:
Dividing on ρ and unfolding the integrals, we can get in both cases the following equations for ∆:
So, we have correlation which defines the position of MC in relation to back end of the head through the head’s length, and ratios of densities (m) and lengths (k) of the head and the tail. Note that, as m and k coefficients are positive, the sign of ∆ is determined by numerator. I.e., MC is inside the tail (∆ > 0), if k>m-1/2, and it is inside the head (∆ < 0), if k<m-1/2. Now, substituting (4) to (1), we have following square inequation:
k2·m+k·(3m-1)+1 ≤ 0 (5) As we know from the school mathematics, the condition of its real solutions is nonnegative discriminant, i.e. (1-3m)2 - 4m≥0 (6) This leads to
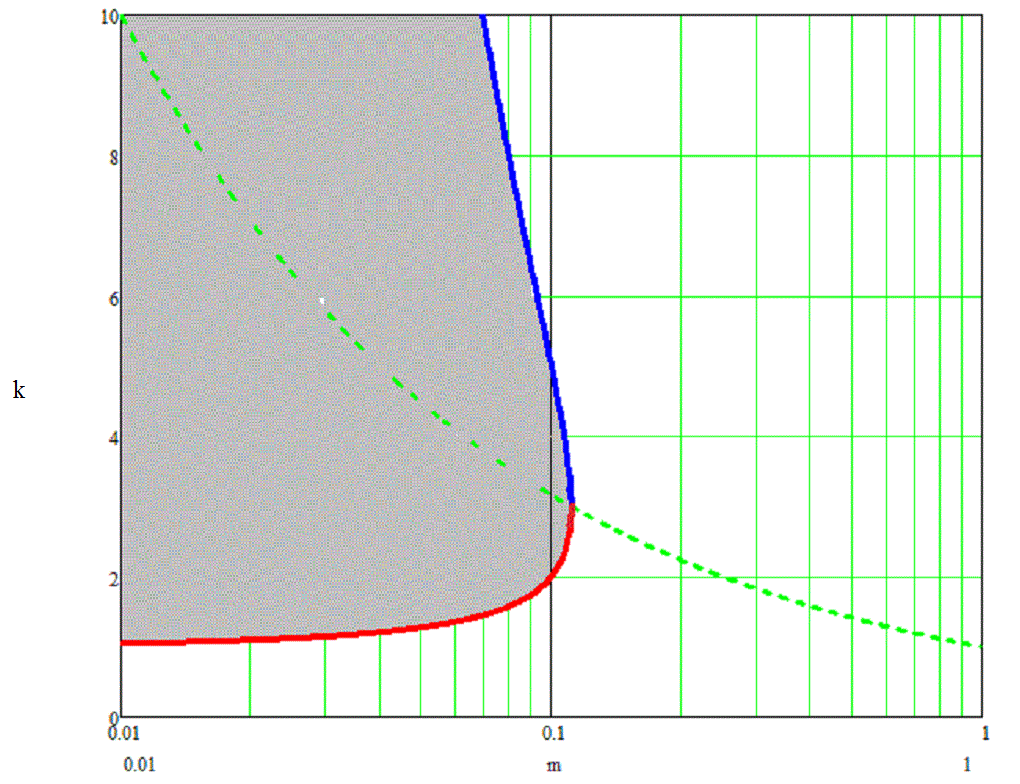
(the second solution m>1 is incidental, because the material of the tail is less dense than one of the head according to preconditions of our problem). Thus, we have an important conclusion: density of the tail for unfinned arrow must be, at least, 9 times less than the density of the head. Solution of inequation (5) looks like range of values of arbitrary tail length:
The origin of this range is intuitively clear – too short arrow (small k) is not aerodynamically stable, and for too long one (big k) its tail mass will be equal and more than one of the tip, which leads to disappearance of MC shift to head part of the projectile (necessary condition of the stabilization). The solution above is visualized in figure below:
Fig. 3. Region of permissible values of the relative length k of the tail (grey colored) in dependence on density ratio of the tail and the tail m.
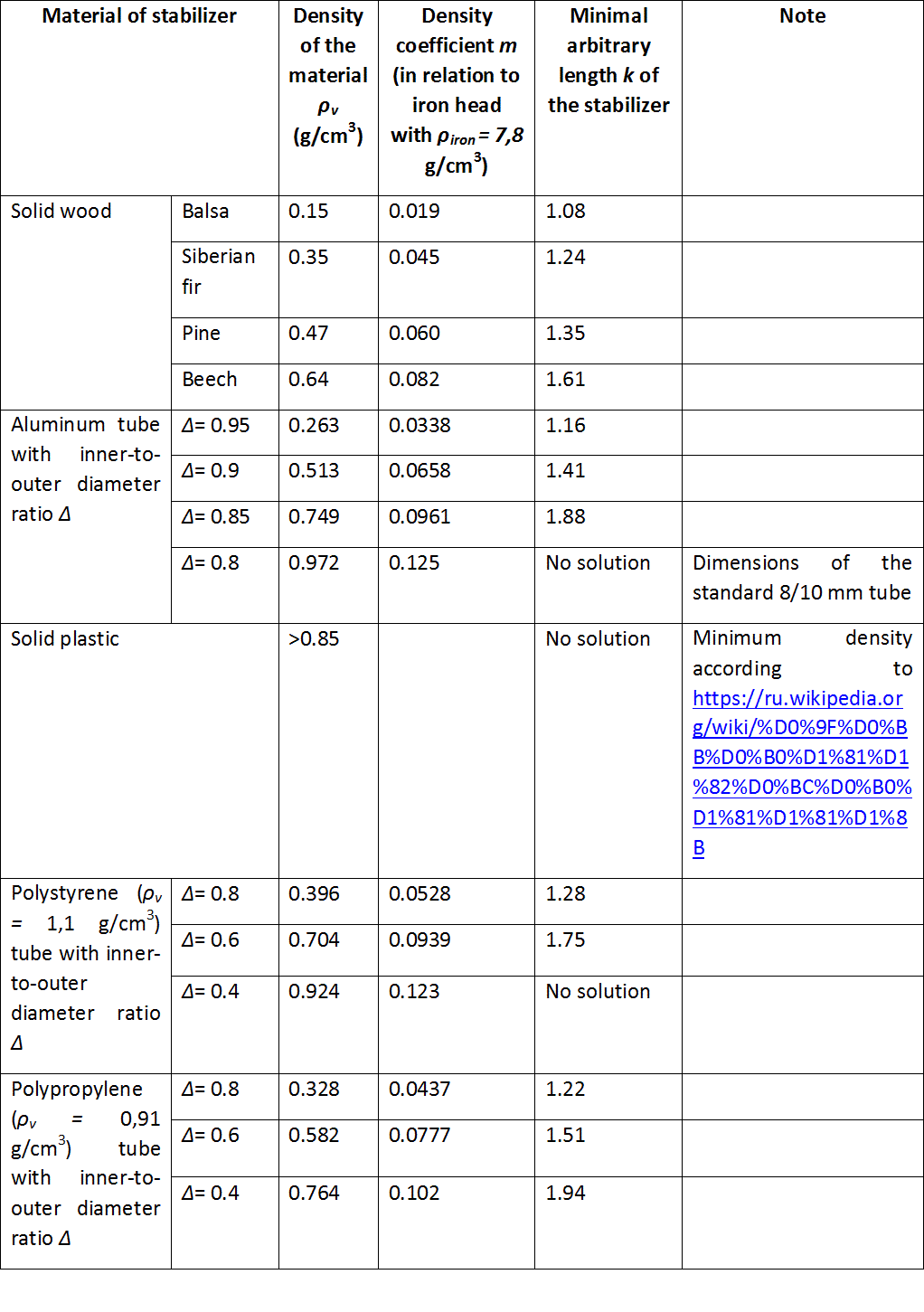
Dashed line k = m1/2 divides the graph to 2 parts: in upper one MC is outside the head, in lower one - inside it. It is demonstrated that there is no solution when m>0.11 (according to (7)), and in this point minimum length of stabilizer is 3 times the length of the head, independently of their materials. Thinking about application of these results in electromagnetic accelerators, we should obviously focus on the case of minimal length of arrow, as it ensures minimal «parasitic» mass of tail and, hence, maximum acceleration efficiency. Table below contains minimum length of stabilizer (in a form of k coefficient) for different materials (according to solution of (8)) providing stable flight of iron-headed arrow.
The table provides us with some interesting and useful conclusions. First, it becomes clear that all sorts of wood can be utilized as solid cylindrical stabilizers (even as dense as beech). On the contrary, none of plastics can be used as solid stabilizer. Second, considering tubular stabilizers we should keep in mind their inside-to-outside diameter ratio (i.e. thickness of a tube). This ratio must be more than 0.8 for aluminum, which corresponds to standard 8/10 mm tubes widely spread in stores. At the same time, the ratio is worse (less) for thinner tubes, so we can conclude that standard aluminum tubes are not appropriate for stabilizing projectiles of less than 10-mm caliber. On can also note that archery and crossbow arrows use special thin-wall aluminum tubes (even finned one). As for plastic tubes, the restrictions on their thickness are quite softer. At last, as one can see from the table, the stabilizer two times longer than head is enough in most practical cases. | |
| Views: 771 | |
| Total comments: 0 | |
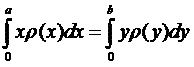
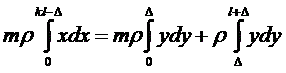 (3a)
(3a)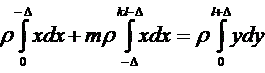 (3b)
(3b) (4)
(4)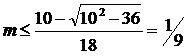 (7)
(7) 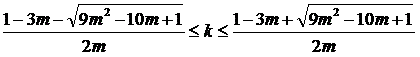 (8)
(8)