As a coilgun is by definition an accelerator of a ferromagnetic body, it is necessary to answer a question before considering its main properties – what is a force of attraction between the coil and the ferromagnetic? To do this, we should get a deeper view into physics.

A modern theory characterizes the magnetic field by two parameters: induction (flux density) B and field strength H (they are vectors, i.e. have directions in space but we will omit these difficulties here). H describes a field generated by macro-currents (i.e. ordered movement of electrons in wires), and B concerns total field born by both macro- and micro-currents (i.e. disordered charge carrier movement in a medium). These two values are connected by a following relation:

B = µ·µ0·H

(1)

where μ is magnetic permeability of a medium (it speaks about the soild’s ability to magnetic polarization, i.e. orientation of micro-currents by an external field), and μ₀ is proportionality coefficient having different value and dimension in different number systems.

The most of media (diamagnetics, paramagnetics) has μ very close to unity, thus their microcurrents weakly react to the field and the force of their interaction with a magnet is negligible (however it can be detected in some interesting experiments). Ferromagnetics (the most well known of them is iron) behave in another way – they consist of the regions with co-oriented microcurrents inside (so called domains), which are able to order and join in such a way that even in a weak external field the inductance becomes huge. This process is illustrated on the pictures below (the latter two taken from James Paul’s site).

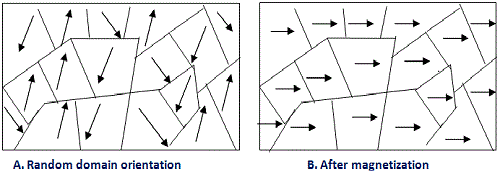	Magnetization of ferromagnet in external field
	Disordered microcurrents in ferromagnetic without an external excitation
	Orientation of the microcurrents

Fig. 1. Illustration for the iron magnetization process.

 

As a result, a ferromagnetic’s permeability becomes as shown in fig. 2 on the left, and induction – on the right. One can see that a magnetization by external field re-orients the domains which leads to a steep increase of inductance while the permeability can be as high as thousands. Then (this happens at H~10²  Amp/meter), when nearly all the domains are re-ordered by the field,  μ starts to decrease. This condition in ferromagnetics is called “saturation” and characterized by the value of induction B_нас. The induction proceeds to increase with H after the saturation, but by a “common” way, i.e. because of the external currents.

 

 

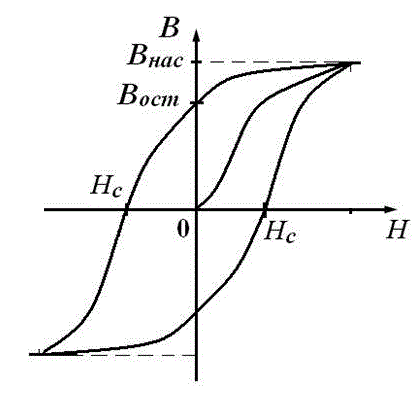Fig. 2. Magnetic permeability (left) and induction (right) vs field strength. Also shown inductance of saturation B_нас and a residual inductance B_ост (it characterizes a field of domains left after the external excitation vanishes). To suppress it a field which equals to Hc must be applied called "coercive force".

 

To visualize these processes we can rewrite (1) as follows:

B = (1+ χ) ·μ0·H = μ0·H+ μ0·M

(2)

where χ is magnetic susceptibility (χ = μ -1), and M is a vector of magnetization of the medium (M = χ·H)

This relation shows clearly that the induction inside a matter is formed both by external and internal currents. In a weak field (before and at saturation) in ferromagnetic μ >>1, so the latter term in (2) may be neglected (i.e induction is nearly completely generated by microcurrents and close to B_нас = μ₀· M_sat where M_sat is magnetization of saturation). In strong fields (more than 10⁶ A/m) vice versa, the magnetization is comparatively low and ferromagnetic behaves as a “usual” matter with field determined by external sources. The fields in the coilguns are in some “mean” range (about 10⁵ A/m) which hampers  the analysis as we cannot introduce any simplifying assumptions (for instance suggesting μ ≈ 1 or B = B_нас).

 Now at last we have enough of theoretical base to answer our title question.

At first, we should examine a relation well-known from literature on magnetism. For example, here the following formula is given for attraction force between an iron core and electromagnet:

F = ½ B2·S / μ0

(3)

where S is the core cross-section perpendicular to magnetic flux.

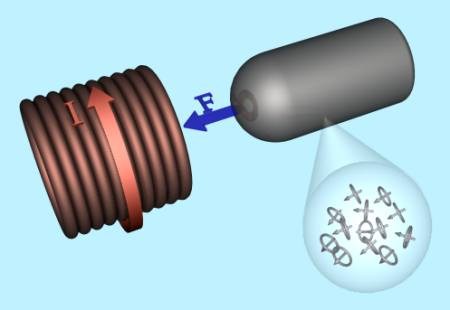
Fig. 3. Horseshoe-shaped electromagnet attracting an iron bar.

 

The latter formula concerns a case when an air gap between the core and the magnet is small, and all the magnetic flux flows through the core (i.e. there is no field outside). Besides, it is suggested that we are on a linear region of B(H) curve before saturation ( ½ multiplier rises from here). It is clear that our case is more complicated, because the field is much stronger and part of it diffuses away an accelerated body.

To obtain more correct relation for the coilguns, let us imagine a coil with current attracting an iron projectile of the length l and cross-section S (see fig. 4). Also shown by red is dependence of the field strength vs coordinate (we will consider the constant in time field to change only along Ox axis).

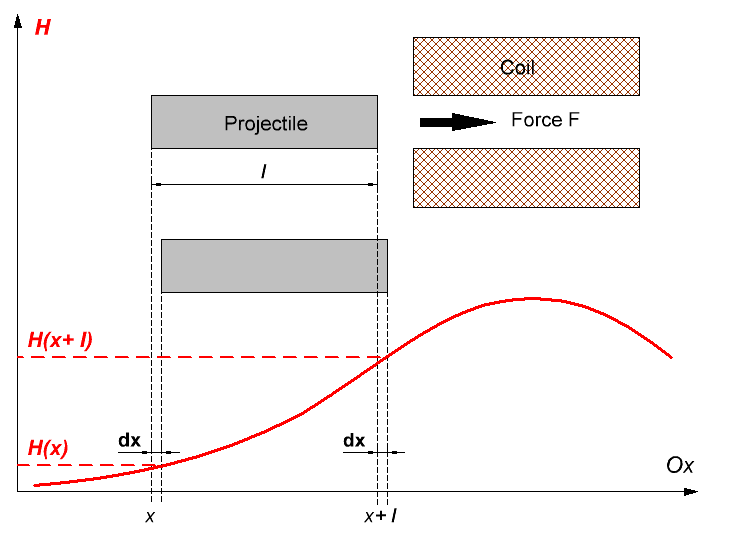
Fig. 4. Force acting on a projectile in coilgun.

 

Physics tell us that force acting on the body is space derivative of the energy of the system with negative sign, i.e. relation of the negative energy change when the coordinate shifts by the infinitely small dx, to this dx:

F = -dW/dx

(4)

 

Fig. 4 reveals that the energy in our system changes only in two places – on the rear and front ends of the projectile. It can be considered as a thin layer with thickness dx is cut from the back and transferred in forward direction to the distance l (the external field for this layer increases from H(x) to H(x+ l) during this procedure). Simultaneously, an air layer of the same thickness is transferred in reverse direction. Supplied the field is weakly disturbed by the projectile (which must be close to reality in high fields), there are no changes in all other volume around the coil, i.e. dW = 0 there.

Further, it is known that magnetic field energy density change in matter at inductance variation has the following form:

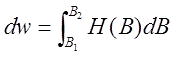(5)

 

Thus, total energy variation will be the sum of its change in ferromagnetic with volume of dx·S while taking it from the flux density B(x) to B (x+ l), and in the same volume of air transferring backwards:

 

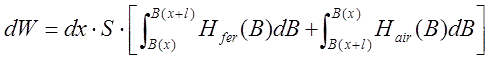(6)

 

here H_fer(B), H_air(B) - field strength vs inductance for the ferromagnet and air, correspondingly. This situation is visualized on fig. 5, where the B(H) curves are schematically depicted for iron (solid line) and air (dashed line). Energy shift in ferromagnetic is a shaded figure.

 

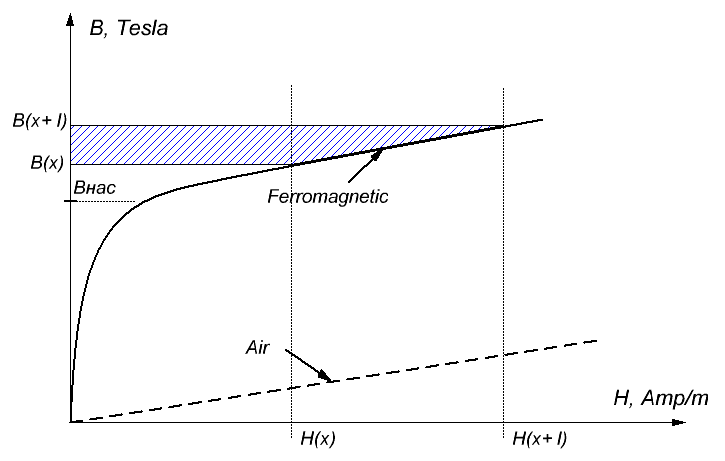
Fig. 5. B(H) curves in iron and air. In high fields, the dependencies go nealy in parallel shifted by B_нас.

 

H(B) functions can be expressed from (2) with the only difference that the second (magnetization) term in air is zero.

So, we at last can obtain for the force:

 

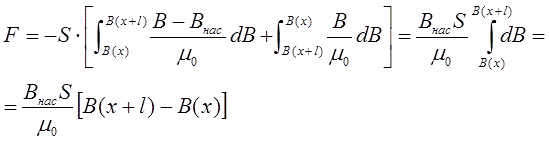(7)

 

Getiing B through H from (1), we finally have:

F = Bнас ·S ·[H(x+ l) - H(x)]

(8)

 

The simplicity of this relation is caused by the fact that all its components can be easily estimated: the core cross-section is determined by the experimenter, its saturation induction is well known for many ferromagnets, and the field strength can be calculated by FEMM or analytically with some formulae given in following sections.

A similar result can be obtained suggesting the projectile as a permanent magnet with dipole moment P.  Then, its interaction with the field will be as given in J.Paul's site:

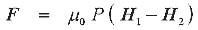(9)

where H₁, H₂ is field intensity on the front and back ends of the projectile. Pictures taken from the same page are below:

 

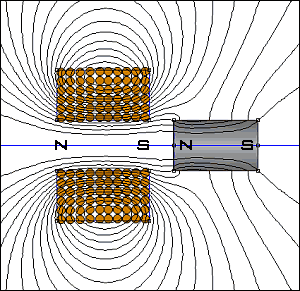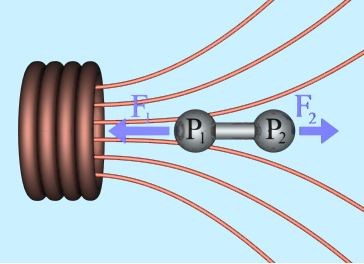Fig. 6. A force acting on a projectile in coilgun as an attraction of permanent magnet to the coil.

 

Thus, we have, at first approximation, an answer to our question: the force of interaction benween a ferromagnetic and an electromagnet is proprotional to the difference of the field intensity on the front and rear ends of the projectile.

This conclusion makes clear that it is necessary to calculate exactly field strength of an arbitrary coil to assess the parameters of electromagnetic accelerator. This is what we will consider in the following publications.

 

Next>

Addition: a calculation in FEMM was conducted to verify eq. (8). Its procedure and resuls are given here. The formula is proved for strong fields inherent to the coilguns.