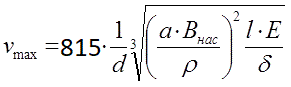| Home » Articles » Theoretical papers » Coilgun calculations |
In a previous paper, following equation was obtained for the maximum achievable velocity in a multistage reluctance accelerator:
Here: a - the dimensionless ratio of the caliber of the winding wire "by copper" to its effective diameter in insulation (usually a = 0.75..0.85 is obtained) Bнас - saturation induction of the projectile material, Tl δ - is the resistivity of the winding conductor, Ohms *mm2/m E - is the electrical energy expended on the shot, J ρ - the density of the projectile material, kg/m3 d - coilgun caliber - inner diameter of coils, cm l - the total length of the accelerating coils, cm. The speed from (1) is obtained in meters per second. Among other things, the derived ratio is important because it allows a comparative assessment of the characteristics of various accelerators. It is necessary to identify optimal designs and determine the most effective engineering solutions for further improvement of gauss guns. However, for such a comparison, it is necessary to establish some criteria by which it will be made. The first thing that comes to mind in this case is the efficiency of the accelerator (i.e. the ratio of the kinetic energy of the accelerated body to the electrical energy expended on its acceleration). However, as E.Vasiliev writes quite rightly, this parameter is not suitable for comparing different coilguns, because it depends on the caliber of the device - a simple increase in the diameter of the projectile gives an increase in its kinetic energy without an increase in speed (and in fact, even with a decrease in it, as can be seen from the above ratios). Obviously, this cannot be considered an "improvement" of the coilgun, therefore, on the same page, the author, noting the paramount importance of the output velocity of the projectile, suggests using a coefficient Kx equal to the ratio of the square of the velocity to the energy spent. In fact, this value is proportional to the efficiency of the coilgun divided by the mass of the projectile, which, in the first approximation, allows you to neglect the caliber of the launcher. This parameter is used on the Arsenal page to characterize the coilguns given there. However, if we continue these reasoning, it becomes clear that the comparison criterion needs significant clarification. Firstly, Kx completely ignores such a parameter as the length of the accelerator (read - the number of accelerating coils). But even a very well-calculated and high-quality one- or three-stage coilgun will have a deliberately smaller Kx than a 10-coil analog assembled "carelessly". Perhaps such a comparison was fair at the time of the formation of the Arsenal (i.e. more than ten years ago), when most of the coils were single-stage, but now almost all designs developed and posted on the Internet are multi-coil by default, and it is quite obvious that the difference in the number of their windings needs to be taken into account somehow. Secondly, as already mentioned, when determining Kx , the author proceeded from the assumption that the velocity of the projectile does not change with increasing its caliber (while maintaining the energy expended), which, as I have shown, is not accurate - it turns out that small-caliber systems will have a "shift" towards large Kx. Finally, since Kx is a purely empirical value, it does not allow us to emphasize certain characteristics of a particular accelerator that affected its value: let's say it turned out that the coilgun is bad (has a low Kx), and what then? What should be done to improve it? To resolve these difficulties, I propose to introduce a new criterion for evaluating coilguns as follows:
Here vmax is the maximum velocity of the accelerator, calculated by (1), and v is the real velocity of the projectile in a particular device. The coefficient G (you can also call it the G-factor, from "geometry") obviously should be in the range from 0 to 1. The greater its value, the better one or another accelerator is optimized (i.e., the dimensions of the projectile and coils, as well as the time diagrams of their operation are selected correctly). G is also convenient to specify as a percentage (then the value calculated by (2) must also be multiplied by 100). To estimate the G-factor of a particular coilgun, it is necessary to know all the values included in (1). Unfortunately, there are very few devices for which a complete set of these data is available. This is especially true of the inner diameter of the accelerating coils d - usually the authors indicate only the caliber of the projectile, which can be much smaller. Nevertheless, we can simplify our life a little if we assume that iron shells are used everywhere (Bнас = 2 Tl, ρ = 7870 kg/m3), and the coils are wound with an average density level (a = 0.8). Taking advantage of these simplifications, I started a separate page, where, to begin with, I posted all the accelerators available on the Internet to date, for which there was a sufficient set of information. Along with the calculated value of G, the table also shows the value of Kx , so that in the future it would be possible to somehow evaluate and compare the informativeness of these parameters. I hope that the table will be updated over time - for this I ask gauss-builders to contact me by e-mail eugmit@yandex.ru or through the feedback of the site and report the parameters of their accelerators.
Sincerely Yours,
Note: when deriving the relation (1), it was noted that it is valid under the condition of equidistant motion of the projectile through a great number of stages N. Therefore, only accelerators with at least N=3 stages will be accepted for consideration and evaluation using the G-factor.
| |||||
| Views: 671 | | | |||||
| Total comments: 0 | |