5. Limiting velocity of the projectile achievable in coilgun.
It was shown on the previous page that the highest speed in gauss gun is acquired by an infinitely thin projectile. To estimate this fundamental value, we will use the relations (3) and (8), integrating the force acting on a "pancake-like" projectile of infinitesimal length dx along the acceleration trajectory. In this case, the initial point of this acceleration should be located at an infinite distance from the coil (which maximizes the speed), and the final point is obviously in the center of the winding (i.e., in our notation, at the coordinate x = - ½ c).
Then, according to (13a), for zero initial speed we get:
 |
(15) |
The integral expression here will be equal to just the field in the center of the coil (let's denote it as Hm):

Then, replacing the mass of the projectile in the denominator (15) by its geometric dimensions and density m = p·S·dx, and shrinking the area S and the element of length dx, we get the following simple expression:
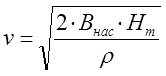 |
(16) |
That is, the maximum velocity of the projectile depends only on the induction of saturation of the material, its density and the field strength in the center of the winding.
If we are talking about a coilgun of a specific caliber d, then we can recall that the strongest field is generated in the center of the so-called "ideal" coil, the length of which is equal to two internal diameters, and the outer diameter is equal to three internal diameters. It turns out that such a winding will give to our "pancake" the maximum speed (it is interesting that this is perhaps the only justified case when the "ideal" coil really provides the optimal coilgun's characteristics). Let's try to estimate it by calculating Hm in terms of geometric parameters and the power of supply using the formulas obtained here.
So, the form-factor (11) in the center of the ideal winding (c = 2d, D = 3d, x = - d) reduces into the following expression:
Then, substituting the corresponding value of H from (5), taking into account its dimension (A / cm) in (16), and reducing all the numerical values, we get finally:
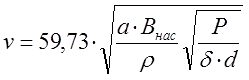 |
(17) |
I would like to emphasize once again the importance of this ratio, because it gives a limiting assessment for the speed characteristics of a (single-stage) electromagnetic accelerator, regardless of the dimensions of the coil, or the length or shape of the core...
For example, for an iron (Внас = 2 T, ρ = 7870 kg/m3) projectile with a caliber of d = 1 cm, accelerated by a copper (δ ≈ 0.0175 Ohms·mm2/m) coil wound "turn to turn" (a = 1), for a power source of 10 kW, we get a maximum speed of 26.18 m/s. This value correlates well with the results shown in Figures 7 and 8.
In addition, the formula (17) allows us to compare the parameters of the coilgun according to the degree of their influence on the output speed. The characteristics of the accelerated body - its density and saturation induction - have the greatest "weight". Equally "influential" is the winding density a. But the caliber of the coilgun and the resistivity of the wire that the coil is wound with are secondary parameters - the speed depends on them only as the root of the fourth degree. Moreover, with an increase in the caliber (while keeping the other conditions constant) the speed decreases.
Finally, the dependence of the output velocity of the projectile on the power of the source is equally weak: v ~ P1/4. That is, to increase the speed of the projectile by 2 times, it is necessary to increase the power by 16 times. For example, to get v = 100 m/s in the above example, you need to have an energy source with a capacity of approx. 2 130 kW (equivalent to a current of 2130 A at a voltage of 1000 V), which is close to the limit even for modern compact thyristors, and much higher than the limit for controlled switches (transistors). Moreover, as we remember, we are talking about "ideal" conditions (an infinitely thin projectile, acceleration from an infinite distance, i.e. indefinitely long) - in real systems, the result will be much more modest...
This confirms the long-known fact that in order to obtain high projectile speeds, it is necessary to use a multi-stage acceleration system. And the most interesting thing is that with the help of the relations obtained above, it is possible to get an estimate for the maximum achievable speed in a multi-stage coilgun... We will deal with this in the next publication.
Sincerely Yours,