3. Limiting value of the kinetic energy of the projectile.

Let's now try to understand what the relations (12) and (14) obtained on the previous page lead us to.

First, we will estimate the maximum energy acquired when drawing projectiles of different lengths into a coil of fixed dimensions. To do this, we will set the caliber of the projectile (the inner diameter of the coil) d = 1 cm and consider an "ideal" winding with dimensions D = 3 cm, c = 2 cm (with such parameters, the maximum field will be generated in the center of the winding at a given current power P). Let's also assume P = 10,000 W (this corresponds to a current of 100 A at a voltage of 100 V, i.e. a coilgun of average power). Then, for a copper wire ( δ ≈ 0.0175 Ohms·mm²/m) wound without gaps (a = 1), we obtain the following graphs:

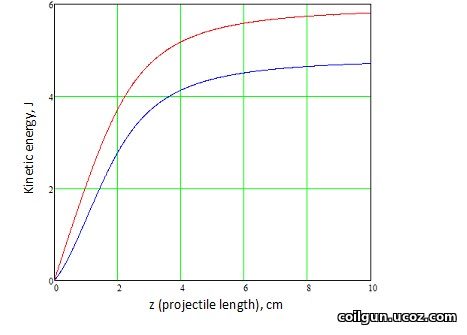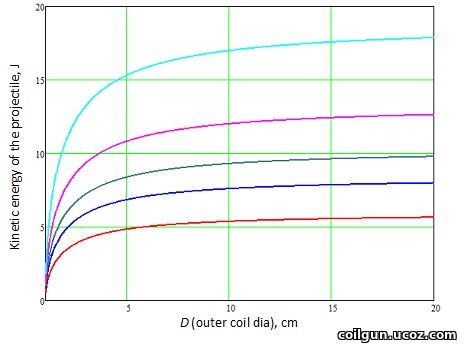
Fig. 4. The dependence of the kinetic energy on the length of the projectile for cases when the front face of the projectile at the moment of acceleration is at an infinite distance from the coil (—) or coincides with the end of the coil (—). This corresponds to Emax and E0 in eq. (12).

 

As you can see, when accelerating from the end, the acquired energy is noticeably less than when starting "from infinity".

In addition, the energy at first sharply, then more smoothly, but monotonously increases with increasing the length of the projectile. According to common sense, this is quite logical, since the accelerating force (1) is proportional to the difference in field strength on the front and rear faces of the projectile, and when the rear face is removed from the coil (i.e - increasing the length of the projectile), it grows. Thus, if the purpose of accelerating a body is to obtain maximum kinetic energy, its length must be expanded.

On the other hand, it can be seen from the graphs that the energy in each case tends to a certain maximum value, which corresponds to a projectile having an infinite length. This value is abstract, but it is interesting to get it explicitly, because it shows the maximum kinetic energy that can be obtained by accelerating a ferromagnet in this particular coil. To do this, it is enough to use the formula (9) again, putting x₂ = -∞, z = ∞ (in this case, in the "geometric" function (10), the first term in the subintegral brackets can be discarded, since it will become zero). Since the length of the projectile z is now equal to infinity, it is reasonable to consider the dependence of the energy on other geometric parameters - the outer diameter D and the length of the coil c (we will not change the other parameters). The calculation result for launching from infinite distance is shown in Fig. 5.

Fig. 5. Infinite projectile's kinetic energy vs outer diameter of the winding with length: — - 1 cm — - 2 cm —-  3 cm — - 5 cm — - 10 cm Acceleration starts from infinite distance.

 

As can be seen, the energy monotonically increases with the growth of the outer diameter and length of the coil. This result is understandable: since the magnetic permeability of the projectile decreases with an increase in the strength H, the most effective way to draw the ferromagnet will be a coil that creates the most " smeared" field in space. For an infinitely long projectile, such a coil will be, respectively, a winding of unlimited dimensions...

Figure 6 shows a similar result for the situation when the acceleration of the projectile begins from the end of the coil. For convenience, the image is given in a logarithmic scale along the horizontal axis.

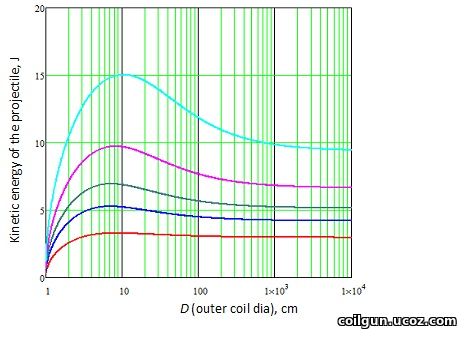Fig. 6. The same as on fig. 5 with acceleration stars from the end of the coil.

The graph differs from the previous one in that for each length of the coil there is now a maximum on the dependence E(D), i.e. there is some optimal winding diameter that provides the most effective acceleration of the core.

The dependences in Fig. 5 and 6 for each fixed length of the winding, with an unlimited increase in D, tend to a certain amount of energy. In principle, it can be derived analytically by directing the winding diameter to infinity (D→∞) in the ratio (12). Since we are now discussing the abstract case of an infinite projectile, I did not bother with this, but an interested reader can try to do these calculations independently. It can only be noted here that this limiting kinetic energy acquired during acceleration "from infinity" is twice as much as for a coil of the same length obtained during acceleration "from the end".

In the next section, we will consider cases of a projectile of limited dimensions that are more close to real life - for them it is possible to estimate the increment not only of energy, but also of speed.

 

4. Dependence of speed of the projectile on its length and on dimensions of the coil.

To begin with, we will depict the increment of the projectile velocity calculated by the ratios (14), depending on its length for the two cases considered above - acceleration "from infinity" or "from the end of the coil", and we consider both the case of an initial velocity equal to zero and 100 m/s.

Fig. 7. Speed increment when the projectile starts from: — - infinite — - end of the coil Dashed are curves for initial velocity 100 m/s. Power 10 000 W, coil outer dia 3 cm, inner dia 1 cm, length 2 cm.

You can immediately notice that when accelerating "from infinity", the maximum speed increment is obtained - this corresponds well to the previous graphs, for which in this case the kinetic energy is also the greatest. An important detail here is the fact that the speed of the launched body increases with a decrease in its length, and it is maximum for an infinitely short projectile.

When moving the starting acceleration coordinate to the end of the winding, a pronounced maximum appears depending on the speed of the projectile length, i.e. for given dimensions of the winding, there is an optimal length of the accelerated body at which it receives the greatest speed (nevertheless, even in this maximum, the speed is less than for an infinitely short projectile in the previous case).

The dependencies for a high initial velocity of the body have the same character (with the only difference that the absolute values of the velocity increment are, of course, smaller here).

If we now vary the dimensions of the winding, we will get a series of graphs that I gave in a publication devoted to the general properties of coils of electromagnetic accelerators. Here, the consideration is limited to the realistic case of acceleration "from the end of the coil" from a rest state.

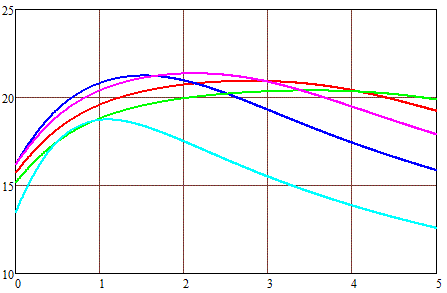
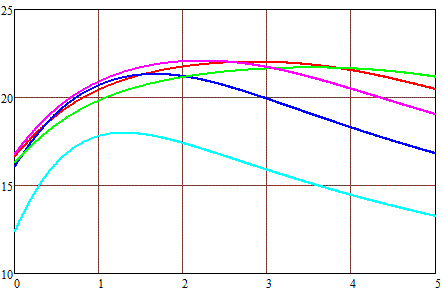
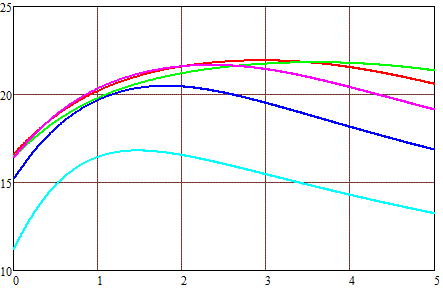
(a)	Fig. 8. Maximal velocity of a 1-cm-caliber projectile (on the vertical axis) depending on its length (on the horizontal one). Outer dia of winding 2 cm (a), 3 cm (b) and 4 cm (c).
(b)	Coil length : — - 1 cm — - 2 cm — - 3 cm — - 4 cm — - 5 cm
(c)

The picture here is similar - for each dimension of the winding, there is an optimal (in terms of speed) length of the projectile. It can be seen that it grows with an increase in the outer diameter and length of the coil. The output speed also increases, but up to a certain limit, and then begins to decrease again. That is, based on the families of curves in Fig. 8, it is possible to determine the dimensions of the winding that gives the maximum speed for each specific shape of the projectile. Or, on the contrary, knowing the geometry of the coil and the coordinate of the acceleration start, you can calculate the optimal length of the core.

Finally, it can be noted that this most optimal length of the projectile is always slightly less than the length of the corresponding coil (unless we consider very thick and short windings, which are already far from the ideal efficiency). This correlates well with the simulation results I have shown here for small and medium power coilguns.

At the end of this publication, I will demonstrate how, using the proposed approach, it is possible to estimate the maximum speed of a projectile achievable in a coilgun (regardless of its design), having data on the power of the power source.

 

<Back

Next>