As shown in the previous article, the problem of optimizing the parameters of the accelerating coil in the coilgun is inextricably linked with the shape of the projectile. Therefore, at the end of this short series of papers, it is necessary to say a few words about the accelerated body, or rather, its optimal shape, which ensures the maximum efficiency of converting electrical energy ΔEelectric into kinetic energy ΔEkinetic (which, in fact, is the main function of the coilgun). To do this, we will once again rewrite the formula we obtained for the force acting on the projectile:
| F = Bнас ·S ·[H(x+ l) - H(x)] | (1) |
where Bнас is saturation induction of the ferromagnet, H - field strength at the front (with coordinate x) and rear end ofthe projectile (having a length of l), S - the projectile's cross-section perpendicularly to the magnetic flux.
Considering a constant electric power P in a coil (which is rather rude approximation because for example current dynamics must be taken into account), an acceleration efficiency η will be proportional to this force:
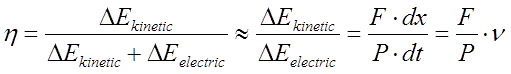 |
(2) |
We can see that the efficiency increases with a speed of the projectile v.
What do these relations give us?
Let's first deal with the length of the projectile.
To do this, note that formula (1) contains in parentheses is the difference in the forces on the front and rear faces of the projectile. So, its optimal length will be such that the "nose" of the projectile is the longest time in the area of the maximum field, and its "tail " - in the minimum one. Then the projectile will be affected by the greatest accelerating force.
From this point of view, an infinitely long projectile will be the most optimal - its back end is always at H = 0 simply because it is infinitely distant from the source of the field - the coil (see Figure 1).
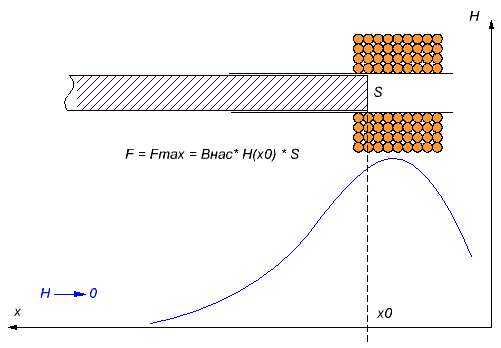 |
Fig. 1. The maximal accelerating force occurs for an infinitely long projectile. Hence, it will get maximum kinetic energy when passing the coil. |
The problem, however, is that according to eq (2) the projectile must have some speed in order to obtain a substantial acceleration efficiency. It is known from the school physics course that when a body receives a fixed amount of kinetic energy, the increase in its velocity is inversely proportional to the mass:
| dE = d (mv2/2) = mv·dv, hence dv = dE / (m·v) | (3) |
Therefore, to accelerate an infinitely long projectile, it is necessary to spend (who would have thought !) unlimited amount of energy...
If we now move from mathematical abstractions to real life, it is clear that growing the length of the projectile above a certain value will no longer lead to an increase in the accelerating force, since the field at its rear end will already be close to zero. At the same time, the mass of the projectile (at a fixed caliber) increases linearly with its length. Therefore, starting from some point, an expansion of the core will begin to cause a decrease in efficiency.
On the other hand, a very short (flat) projectile, although accelerated well, but due to the low mass, the kinetic energy of such a "pancake" will tend to zero.
Thus, it should be expected that for each fixed set of system parameters (the size of the coil, the energy of the capacitors, the initial velocity of the projectile), there will be some optimal length of the accelerated body.
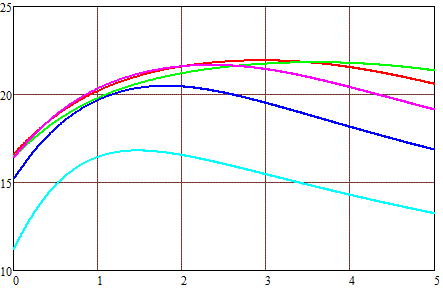
Fig. 2 shows the results of calculations of the maximum velocity of projectiles, depending on their length, achievable when accelerated by an electric current with a power of 10,000 W in a coil with an internal diameter of 1 cm and an external diameter of 2 (a), 3 (b) and 4 (c) cm. For calculations, the formulas for the spatial dependences of the field strength given in the previous article and the value of the iron saturation induction Bнас = 2 T were used. It was assumed that at the moment of turning on the current, the front end of the projectile coincides with the front plane of the coil, and at the moment of turning off, the projectile completely enters the coil (more precisely, the geometric centers of the coil and the projectile coincide - then the retracting force becomes zero). Acceleration is carried out from a state of rest (i.e. from the zero initial velocity of the projectile), while it was believed that the increase and decrease of the current in the winding occurs instantly.
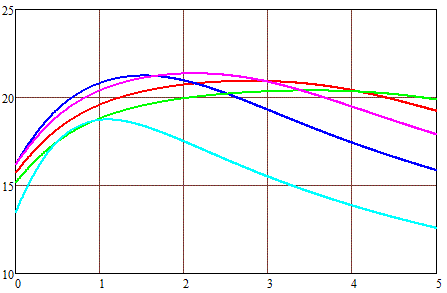 (a) (a) |
Fig. 2. Maximal velocity of a 1-cm-caliber projectile (on the vertical axis) depending on its length (on the horizontal one). Outer dia of winding 2 cm (a), 3 cm (b) and 4 cm (c). |
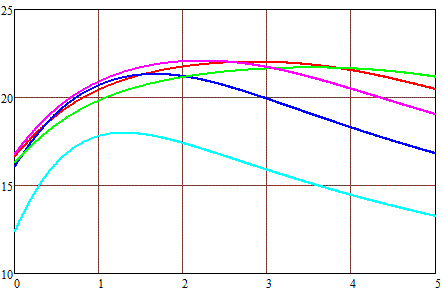 (b) (b) |
Coil length : — - 1 cm — - 2 cm — - 3 cm — - 4 cm — - 5 cm |
 (c) (c) |
These dependencies have some interesting implications, but they will require working with rather complex mathematical formulas, so I will try to analyze them later in a separate publication. In the meantime, we can simply note that for each length of the coil, there is an optimal length of the projectile, which for short coils is slightly longer than their length, and for long coils - slightly less. At the same time, an increase in the thickness of the winding leads to a shift in the maximum speed towards longer projectiles, although the value of this maximum itself changes slightly.
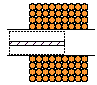
Now let's look at how the diameter of the projectile will affect the acceleration of the projectile (while maintaining a constant caliber of the accelerating coils). To begin with, let's imagine that instead of a cylinder "fitted" to the inner diameter of the coils, we placed a thin rod of the same length l inside the coil (see Figure 3 (a)). How will its speed change?
As shown here, the stress vector within the projectile cross-section changes very slightly, so according to formula (1), the accelerating force will be proportional simply to the cross-section area S. On the other hand, projectile weight, while maintaining its length and material (i.e., density), will also be proportional to S. Because, according to Newton's second law, the acceleration of a body is directly proportional to force and inversely proportional to its mass (dv/dt = F/m), it turns out that "thin" shell will be accelerated exactly the same as "fat." In other words, the velocity of the projectile does not depend on its diameter. But, since the kinetic energy of the projectile is proportional to its mass, the acceleration efficiency of the " thin "rod will be less than that of the"thick" one.
 |
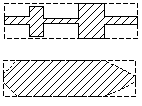 |
Fig. 3. A thin rod is accelerated the same as thick cylinder (a). Different shapes accelerated with a lowered efficiency in comparison to a simple cylinder (b).
It is easy to understand that this reasoning also applies to more complex forms of the accelerated body - any cores that have any narrowing and recesses (see Figure 3 (b)) will reduce efficiency relative to a solid cylindrical body...
The same conclusion can be made on the basis of the simple argument that the core should "collect" the maximum amount of magnetic flux, the generation of which takes all the energy stored in the coilgun. Therefore, it should fill as much of the available space inside the coil as possible, and any deviations from the cylindrical shape allow part of the field to dissipate uselessly.
By the way, it also leads to a conclusion that the walls of the" barrel" of the coilgun ( usually it is just a tube on which the coils are wound outside, and the projectile moves inside) should have a minimum thickness.
Another interesting question is the influence of the so-called "eddy currents", which must occur in the solid body of the projectile when it is exposed to an alternating magnetic field. Since, according to the rule of electromagnetic induction, these currents will be directed opposite to the currents inducing them in the external winding, the resulting force will push the projectile out of the coil. Induction accelerators ("Thomson-gun") work on this principle, but in our case this effect will counteract the acceleration (which in the coilgun occurs, on the contrary, due to the retraction of the ferromagnet by the magnetic field). Among other things, eddy currents can lead to heating of the conductor (which is sometimes used in industry for quenching the surface layers of massive steel parts in special induction furnaces, see Figure 4).
 |
 |
 |
Fig. 4. The origin of eddy cuurents in a massive conductor (left), their mechanical and heat action (right).
To suppress eddy currents, it is often proposed to make a projectile in the form of a set of flat insulated layers (like the cores of power network transformers), or to make a longitudinal cut in it to the central axis. The use of non-conductive materials such as ferrite (like in magnetic cores of high-frequency transformers) is not suitable in our case, because they have a low value of the saturation induction Bнас.
However, when working with an amateur coilgun, it is difficult to notice the effect of eddy currents - most experimenters agree that they do not manifest themselves in any noticeable way in coilguns. More serious experiments and attempts of calculation using numerical simulations confirm this fact. In the article [2], a comparative experiment is carried out on firing a multi-stage accelerator with a solid projectile and a projectile with a longitudinal groove. The latter is actually accelerated a little better, but this difference is quite small (the increase in efficiency was from 2.23% to 2.40 %). B. Slade, based on the results of the calculation in his original simulator, established [3] that the influence of eddy currents on the speed is insignificant, but increases when an external (stationary) magnetic core is introduced into the system. However, the installation of such a magnetic circuit in a powerful coilgun is not appropriate, as I have shown in these works.
As for the heat losses, they are calculated in the core of the coil accelerator in a publication [1].
Many beginners come up with the idea of using a strong permanent magnet (for example, neodymium) as an accelerated body. This desire, apparently, arises on the basis of interest for low-power shooting games based on a chain of permanent magnets, a great many of which can be found in Internet (by the way, these are what were originally called "Gauss guns").
 |
Fig. 5. "Classic" Guass gun with permanent magnets. |
Indeed, the range of magnets is now quite large, and they can be purchased in a convenient (for use as projectiles) form of rods of almost any caliber and length. The problem here is that the fields of such magnets, although they seem large, are inferior to the fields that are present even in weak coil accelerators. Therefore, a pre-magnetized accelerated body will have an advantage only at the initial moment of acceleration, when the current in the windings has not reached significant values - then any ferromagnet goes into saturation, and the value of Bнас begins to play a more important role. And since the saturation induction of magnetically rigid materials used in permanent magnets is usually much less than that of simple iron, there is no benefit from using them in coilguns...
A proposal to use special alloys with an increased value of Bнас as the material of the projectile looks more sensible. So, the permendur alloy consists of 30-50 % cobalt, 1.5-2 % vanadium and the rest-iron. It has the highest saturation induction of all known ferromagnets, up to 2.43 Tesla. Unfortunately, such materials are too expensive and "hard to get" for amateur experiments. Since the projectiles are only consumables, the expediency of the associated costs is questionable, despite the fact that the projected increase in the efficiency of accelerators in the case of their use is not so great.
In conclusion, it is worth noting that in addition to the considered issues of optimizing the acceleration of the projectile inside the coilgun, there is also a separate problem of the behavior of the projectile at the stage when it has already left the accelerator barrel and is moving towards the target in the external environment (in weapons theory, this section is called "external ballistics"). Very little attention is paid to this topic in relation to Gauss-guns. For example, the issues of projectile stabilization in flight are almost not studied. The only exception I know of is the same publication [2], which separately studied the effect of aerodynamic stabilizer on the stability of the core trajectory. Your humble servant also made a contribution by publishing a couple of articles on this site.
A characteristic feature of the coilguns in this part is the fact that the shape of their projectile strongly affects the efficiency of acceleration (which is not present, for example, in firearms or pneumatic weapons), so here the experimenters in a certain sense "have their hands tied".
Another point that is not fully clarified is the optimization of the shape of the front part of the accelerated body. The projectile must be not only accelerated to the maximum speed and reach the target, but also penetrate it to the maximum depth. At the same time, the shape of the nose in the form of a flat face, optimal in terms of acceleration, obviously does not give the projectile a good striking ability.
Conclusions:
1) The optimal length of the accelerated body from the point of view of efficiency should be selected for a specific fixed set of system parameters (the size of the coil, the energy of the capacitors, the initial velocity of the projectile). The longer is the length of the accelerated body, the higher its kinetic energy increment.
2) The acceleration of a core does not depend on its diameter. Therefore, to obtain maximum efficiency, it is advisable to use cylindrical shells that fill the internal volume of the coil as much as possible.
3) As a material for the projectile, ordinary iron is best suited. Since eddy currents in coilguns do not manifest themselves noticeably, taking measures to suppress them (for example, making a projectile in the form of a layered structure) is impractical, as is the use of any special expensive materials with increased saturation induction.
Literature.
[1]. H.Chen et al, "Iron Loss Analysis of Double-Sided Linear Switched Reluctance Launcher", IEEE Trans. on Plasma Science, May 2019, vol. 47 (5), p. 2323.
[2]. H.Xiang et al, "Design and Experiment of Reluctance Electromagnetic Launcher with New Style Armature", IEEE Trans. on Plasma Science, May 2013, vol. 41 (5), p. 1066.
[3]. http://users.skynet.be/BillsPage/SimulationResults1.0.pdf
[4]. S.Kim and J.Kim, "Optimal design of a coil gun projectile by analyzing the drag coefficient and electromagnetic force on the projectile", Journal of Mechanical Science and Technology, vol. 34 (7), 2020, p. 2903.